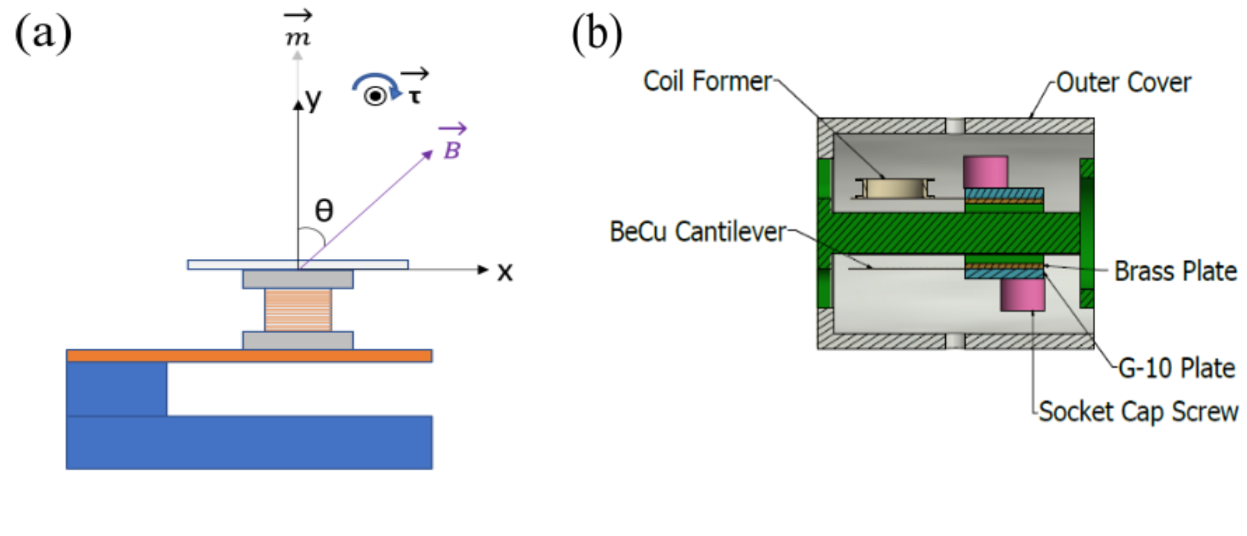
Capacitive torque magnetometry: a sample is mounted on a flexible CuBe cantilever, and this cantilever forms the top plate of a parallel plate capacitor. The device is placed in an applied field and can be rotated. The external applied field that is not parallel to the magnetization in the sample will exert a force to try to align that magnetization with the field. This generates a torque, which will deflect the cantilever, thereby changing the capacitance of our parallel plate capacitor as the top plate gets closer or further from the base plate. The change in capacitance as the sample is rotated in field is therefore directly proportional to the torque. We can use a small home-made coil to calibrate the cantilever, to mimic a sample of known magnetization based on the applied current. Using such a coil the sensitivity of the cantilever can be assessed. Our home-made device allows measurement of two samples at the same time.

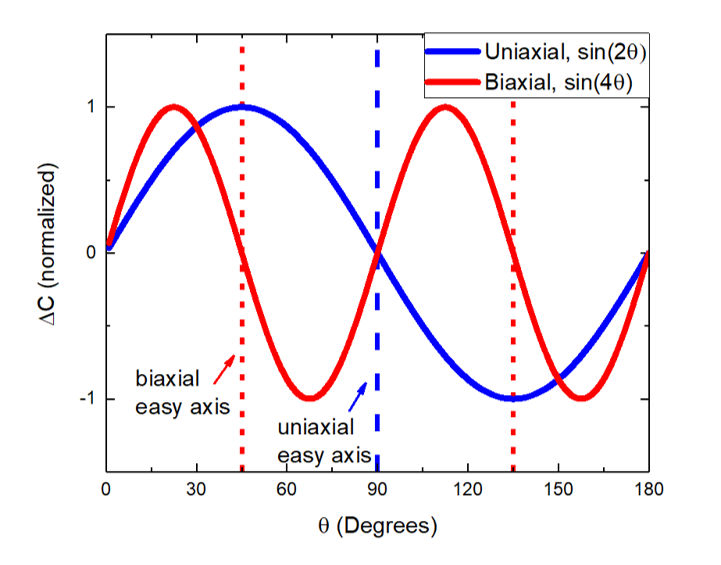
Here we breifly describe the ideal case in which magnetization is saturated along the field direction at all times as the field is rotated with respect to the sample. In this case the torque response is a direct measurement of the strength of the magnetocrystalline anisotropy in the material, i.e., the relative strength and direction of the easy axes. Depending on the symmetry of the crystal and the direction of the easy axes the anisotropy can be uniaxial (easy axis every 180°) or biaxial (easy axis every 90°)

The single-ion anisotropy and magnetic interactions in spin-ice systems give rise to unusual non-collinear spin textures, such as Pauling states and magnetic monopoles. The effective spin correlation strength (J_eff) determines the relative energies of the different spin-ice states. With this work, we display the unique capability of capacitive torque magnetometry (CTM) in characterizing the magneto-chemical potential (MCP) associated with monopole formation. We build a magnetic phase diagram of Ho₂Ti₂O₇, showing that the field-induced magnetic phase transitions cannot be described by a single value of J_eff. Rather, the MCP depends on the spin sublattice (α or β), i.e., the Pauling state, involved in the transition. Monte-Carlo simulations using the dipolar-spin-ice (DSI) Hamiltonian support our findings of a field-dependent MCP, but the model underestimates J_eff for the β-sublattice. The inclusion of long-range exchange terms in the Hamiltonian is needed for a full description of spin ices.

For more information see: Naween Anand, Kevin Barry, Jennifer N. Neu, David E. Graf, Qing Huang, Haidong Zhou, Theo Siegrist, Hitesh J. Changlani & Christianne Beekman
Nature Communications volume 13, Article number: 3818 (2022)
"Investigation of the monopole magneto-chemical potential in spin ices using capacitive torque magnetometry"